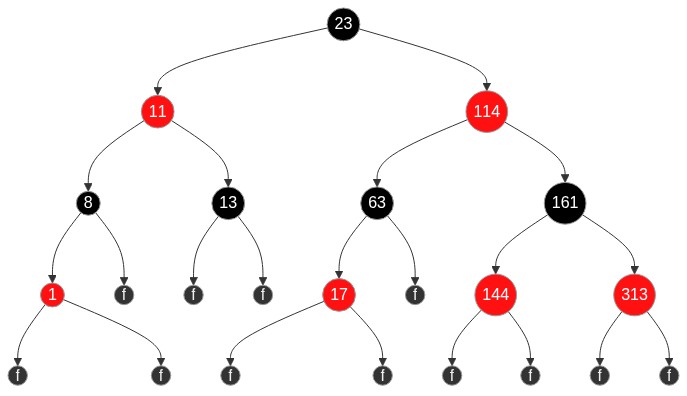
二分查找树在二叉树的基础上实现了插入数据排序,而实现了查找功能.
而自平衡二分查找树在二分查找树的基础上实现通过自旋转实现平衡,以避免树高度过大出现查找复杂度退化为链表.Balance Binary Search Tree.
红黑树算自平衡二分查找树的一种,但其并不完全满足其要求只相对满足其完全的功能,以降低维护的成本,但最坏情况下两个分支高度差不会超过两倍.
红黑树属性
- 节点是红色或黑色.
- 根节点必须是黑色.
- 叶子节点都是黑色空节点.
- 红色节点的两个子节点都必须是黑色(不允许存在连续的红色节点).
- 从任何节点出发到叶子节点路径上黑色节点的数量必须一致.
- 红黑树是自平衡二分查找树,也就是说二分查找树的特征都保留,而其颜色属性就用于平衡树高度,以防止数据结构查找修改复杂度退化为链表.
红黑树的插入操作
红黑树插入是先按二分查找树的规律将新节点插入到树叶子节点,再对新节点所在关注点进行调色与旋转操作以满足颜色属性.所以这儿的操作都在已实现二分查找属性基础进行.同时为了减少插入带来的属性违背,新插入的节点都默认为红色.
插入操作所有的情形有以下5种:
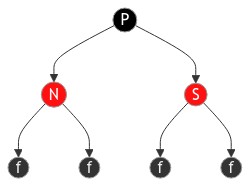
以下操作默认使用P代指父节点,N为新插入节点,S代表兄弟节点,G代表祖父节点,U代表叔父节点,f代表叶子节点.
插入节点是根节点
如果插入的节点位置在根上,这是最简单的插入情况,直接将节点颜色改为黑色,不会违背任何一项红黑树属性.
插入节点父节点是黑色的情况
插入节点的父节点是黑色,此时不需要任何调整,所有原则皆满足.不增加黑色节点,任何路径上黑色节点数量不变,也没产生新的连续红节点.因为叶子节点始终是黑色加在新节点后面不会增加.同时,因为属性4的存在,新加节点分支不可能退化到相邻分支的2倍长度.
插入前:
note:排除以上两种情况后,这个时候父节点只是红色,同时祖父节点必定是黑色,否则会违背属性4出现两个连续的红色节点.
叔父节点是红色的情况
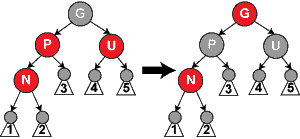
插入新节点的叔父节点是红色(排除以上两种的情况后,这个时候父节点也是红色,也就是说上一层两个节点与当前节点都是红色).到目前为止,除当前新节点外,树的颜色原则是保持得很好的,新节点的插入打破了原则4(有连续的红色节点).这个时候出现的并排的红色节点只需要两个颜色一起改变(也就是直接将父节点与叔父节点颜色变为黑色)即可将当前节点的原则4修复,这样做产生了新的黑节点,为了维持原则5同时两个变色的节点为兄弟节点,只需要将这两个节点的父节点变为红色即可修复当前节点层的原则5(这时原节点的祖父节点的变色带来的问题又放在不同的Case中一直递归到根节点).这样一直递归到根节点(根节点为黑色不修改而让产生的黑色节点最终放在了根节点而作用在所有的路径上),将所有节点的原则5修复.
note:接下来的出现的情况只剩下叔父节点为黑色,父节点一层的颜色不一致.同时当前节点的父节点要么是在祖父节点左边要么在祖父节点右边,两类情况都使用旋转修复,方向相反而已.这个时候要修复原则4,只需要将两个红色节点变成兄弟节点即可(因为成为兄弟节点后,即不是连续红节点,也不增加黑色节点).
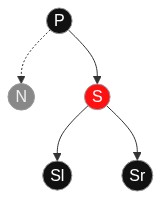
插入节点与父节点不在同一方向的情况

如图所示:在新节点插入后,产生了两个连续的红节点(不在同一方向),这时要做的仅仅是将两个红节点旋转到同一方向以进入到第五种情况.
- 左旋(如果父节点在祖父节点右节点,当前节点在父节点左节点则使用右旋)当前节点与父节点,使当前节点与父节点祖父节点在一个方向上(以方便后一步骤旋转祖父节点与父节点)进入后一种情况:插入节点与父节点在同一方向
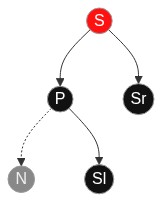
插入节点与父节点在同一方向的情况
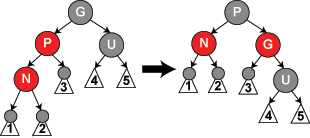
除 Case4 外, Case3 与直接刚插入新节点时都可能直接进入到 Case5 中来.
- 右旋/左旋祖父节点与父点
- 交换原父节点与原祖父节点颜色(原祖父节点颜色只会是黑色),这个时候原祖父节点成当前节点兄弟节点,原父节点成为节点的父节点,交换颜色即将原祖父节点变为红色,而原父节点变为黑色.达到的效果是,当前节点分支不再有连续红节点,也没有增加黑色节点,兄弟节点分支增加了一个红色节点,并不增加黑色节点.
走到这一步骤插入完成,此外, 其他步骤都有可能直接完成插入.
红黑树的删除操作
基于二分查找树删除操作(在二分查找树中,各节点已经排序好删除一个节点只需要将其左分支最大的节点或右分支最小的节点替换到被删除的节点即可),红黑树删除某个节点可以直接转换为复制这个节点替换被删除节点,再将被复制节点删除.而作为分支上左分支上的最大节点或右分支上的最小节点,最多只有一个方向上相反(此处为方便理解不考虑空叶子节点,如果是替换左分支最大节点这个子节点就是替换节点的左子节点,如果是右分支最小节点删除就是此节点的右子节点)的子节点,因此删除操作剩下工作仅仅是删除这个最多有一个子节点的节点.
接下来的讨论只针对删除这个最多一个子节点的节点.从头到尾穷尽此节点的情况与实现树平衡的步骤:
以下讨论内容涉及到黑色节点数量时都不包含空叶子节点.同时,为方便理解假设原删除节点使用的是右分支的最小节点覆盖,在使用左分支的最大节点的情况下,左旋与右旋对调即可.
最简单的情况:当这个被删除的节点是红色的
这种情况下,因为其最多只有一个子节点(不考虑空叶子节点),所以此红色节点没有有效的子节点(其子节点不能为红节点,但如果有一个黑子节点,其违背了原则5黑色节点数量不一致).这个时候直接删除该节点不会违背任何原则:既不会产生相邻红节点,也不会增减任何分支的黑色节点数量.
note:剩下的情况都是被删除节点是黑色的
另一种简单情况:被删除节点是黑色,同时其有一个红色子节点
这种情况下,被删除的分支减少一个黑色节点,违背原则5,只需要将被删除节点子节点移动到被删除节点,同时改变此节点颜色为黑色即修复.
Note:被删除节点除以上两种情况后,只剩下此节点是黑色且无子节点.要满足原则5,兄弟分支到叶子路径上必有一个黑色节点,可能的情况包括:有且只有一个黑色兄弟节点/黑色兄弟节点有两个红子节点/红色兄弟节点有两个黑色子节点.
其兄弟节点没有子节点

这种情况下,兄弟节点没有子节点那么其颜色只与被删除节点一致为黑色才能满足原则5(黑色节点数量一致).
在原则5条件下,此时被删除节点所在分支与兄弟分支到叶子节点的黑色节点数量都为1(排除叶子节点),在删除被删除黑色节点后,其所在分支黑色节点数量相对其兄弟分支少1(破坏原则5).
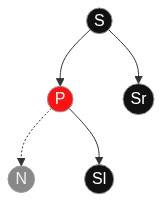
如果父节点P不管是红色还是黑色,什么都不需要做,删除分支直接舍弃,如果没有兄弟分支其本身颜色原则不被破坏,如果有兄弟分支,其原有的平衡也不会被破坏(因为删除节点分支已不存在不需要考虑黑色节点数量原则与红色节点不连续原则).
红色兄弟节点有两个黑色节点
在满足原则4(红色节点不连续)情况下,父节点P只能是黑色.当删除节点N后,需要在左分支添加黑色节点,因此操作是:
- 以P为轴左旋节点P与S,旋转后效果:
- 左旋后,再将原父节点P与原兄弟节点S颜色互换以满足原则5.颜色互换后效果:
黑色兄弟节点有两个红子节点(红色父节点)
- 先以P为轴左旋.左旋后结果:
- 节点P/S/Sr 颜色都取反以满足原则4(红色节点不连续)与原则5(黑色节点数量相同),调色后效果:
黑色兄弟节点有两个红子节点(黑色父节点)
- 以P为轴左旋,左旋后效果:
- Sr节点颜色涂为黑色.调色后效果: